CASOPIS REPUBLICKE AGENCIJE ZA TELEKOMUNIKACIJE

SADRŽAJ

Količina informacija koju je potrebno preneti u komunikacionim mrežama postaje sve veća. Istovremeno, kapaciteti čvorova zaduženih za prenos podataka ne mogu se ravnomerno i stalno povećavati. Sa porastom generisanog saobraćaja u određenom trenutku pojaviće se problem zagušenja. Danas je veoma aktuelno pitanje kako obezbediti slobodan protok u mreži, odnosno kako sprečiti zagušenje. U ovom radu analizirane su različite metode za optimizaciju kompleksnih mreža, tako da se prosečan stepen povezanosti i ukupan kapacitet mreže ne menjaju. Naglasak je na efikasnom rutiranju. Poredili smo različite strategije rutiranja primenjene na akademske mreže u Holandiji i Francuskoj, kao i na mreže generisane pomoću dva generička modela realnih mreža, Barabási-Albert modela mreže bez skale i mreže bez skale na rešetki. Mreže koje imaju neravnomerniju raspodelu opterećenja zahtevaju viši stepen diskriminacije čvorova sa velikim opterećenjem. Predložen je dinamički algoritam rutiranja koji se zasniva na informacijama o trenutnom opterećenju u čvorovima. Rezultati simulacija su pokazali da se izborom adekvatnog algoritma rutiranja, opterećenje u mreži može značajno redukovati.

Ključne reči: kapacitet mreže, rutiranje, mreže bez skale

Study of routing strategies in the small complex networks

Jelena Smiljanić, Milan Žeželj, Igor Stanković*, Scientific Computing Laboratory, Institute of Physics, University of Belgrade

igor@ipb.ac.rs

ABSTRACT

The quantity of information transferred in the modern telecommunication networks is increasing. At the same time, operators can neither gradually nor infinitely increase the capacity of the nodes. The congestion is therefore inevitable as a consequence of the high information traffic rates. Due to its practical importance, the problem of reducing congestion has recently drawn an attention of researchers. In this work, different routing strategies are analysed and compared, which do not change topology of the network. The focus is on efficient routing. The routing strategies are compared using two generic models, i.e., Barabási-Albert scale-free network, scale-free network on lattice, and academic networks of the Netherlands and France. The more inhomogeneous networks require stronger discrimination of the nodes with high betweenness. We propose a dynamic routing algorithm utilizing information about current load of the nodes. The simulations show that by choosing adequate routing algorithm the congestion can be greatly improved, and even removed.

Keywords: network capacity, routing, scale-free networks

1. UVOD

Razumevanje strukture i kontrola komunikacije u kompleksnim mrežama su važni za moderno društvo. Od velikog interesa je kako obezbediti slobodan protok informacije kroz mreže, odnosno protok bez zagušenja [1–13]. Zagušenje u mreži razvija se brzo sa povećanjem broja generisanih paketa. Do zagušenja prvo dolazi povremeno u najopterećenijim čvorovima, a potom i u ostalim čvorovima.. Kritična vrednost poslatih paketa kod koje dolazi do zagušenja zavisi od veličine mreže i kapaciteta čvorova. Maksimalna vrednost protoka informacija koji se može ostvariti pre nego što mreža postane zagušena predstavlja meru kvaliteta njene organizacione strukture. Intuitivno, zagušenje možemo u velikoj meri smanjiti ili izbeći sa veoma velikim stepenom povezanosti čvorova i/ili velikim kapacitetom za prenos paketa podataka. Oba rešenja u praksi bi značila veliki trošak za unapređenje infrastrukture, što često nije ekonomski opravdano [14, 15]. Zbog toga, od velikog značaja je pronalaženje optimalne strategije za usmeravanje saobraćaja pri utvrđenoj strukturi mreže.

Široko korišćena strategija za usmeravanje saobraćaja u mrežama je rutiranje po najkraćim putanjama (pod „najkraćom“ putanjom ovde se podrazumeva putanja sa najmanjim brojem linkova) [16]. Ipak, rutiranje po najkraćim putanjama često ne obezbeđuje dobar kvalitet servisa. Sa razvojem tehnologije, sve više su dostupni empirijski podaci koji nam dozvoljavaju razmatranje cene linka. Cena koja se plaća za korišćenje linka može da odražava različite fizičke karakteristike ili ograničenja realne mreže. Ovde će biti razmotreno kako performanse mreže mogu biti unapređene primenom odgovarajućeg protokola za usmeravanje, bez promene osnovne strukture mreže. Cena linka biće zato korelisana sa topološkim osobinama mreže koje određuju kvalitet komunikacije u njoj. U pogledu dinamičkog rutiranja, u ovom radu ćemo demonstrirati način za raspodelu opterećenja u vremenu u zagušenim čvorovima. To znači da će paket koji nailazi na zagušen čvor duž svoje putanje biti vraćen za jedan korak. Dinamička strategija rutiranja predložena u ovom radu, koristi višak kapaciteta koji postoji u mreži za privremeno skladištenje informacija dok se zagušeni čvor ne oslobodi. Time se izbegava korišćenje bafera što je posebno interesantno za optičke mreže [17].

U poslednjoj deceniji uveden je niz modela sa željom da se kompleksne mreže precizno opišu [18]. Posebna pažnja posvećena je mrežama koje su realizovane (smeštene) u realnom prostoru. U ovom radu koristili smo standardni model mreža bez skale [19] i mreža bez skale na rešetki [20], čije su osobine detaljno proučavane i koje veoma dobro reprodukuju strukturne osobine, kao i komunikacione karakteristike malih telekomunikacionih mreža [21]. Zahvaljujući sličnosti sa realnim mrežama, možemo testirati algoritme za rutiranje na velikom broju topološki različitih generičkih mreža sa sličnom prosečnom povezanošću, kapacitetom čvorova, i ukupnim brojem čvorova. Tako dobijeni rezultati testiranja i zaključci su opšti, tj. važe za bilo koju realnu mrežu slične veličine. Posmatraćemo radi poređenja i dve realne mreže: nacionalnu akademsku mrežu (National Research & Education Networks ili NRENs) Francuske [22] i Holandije [23]. Na izabranim generičkim i realnim mrežama demonstrirana je efikasnost statičkih i dinamičkih strategija rutiranja, kao i mogućnost kombinovanja ove dve vrste rutiranja da bi se ostvarilo najveće moguće poboljšanje performansi mreže bez promene njene topologije.

2. MODELI MREŽA

Barabàsi i Albert prvi su primetili da je postojanje visokog stepena samoorganizacije globalno svojstvo složenih mreža [19]. Da bi opisali svoja opažanja uveli su model mreža bez skale (scale-free) zasnovan na dva ključna principa: (i) verovatnoća povezivanja novog čvora sa postojećim čvorovima nije uniformna i (ii) verovatnoća da će čvor biti povezan sa novim čvorovima je veća ako iz čvora polazi veliki broj veza. Prema Barabàsi-Albert (BA) modelu, mreže bez skale nastaju u nizu koraka u kojima se novi čvorovi sa uključuju u postojeću mrežu. Algoritam počinje sa malim brojem (N₀) čvorova, i u svakom koraku novi čvorovi sa mveza se dodaju i povezuju sa postojećim čvorovima u sistemu. Model pretpostavlja da verovatnoća uspostavljanja nove veze sa čvorom i zavisi od njegove povezanosti k_ii iznosi . Time je u model uključena verovatnoća povezivanja koja zavisi od broja postojećih veza pojedinačnih čvorova. Posle određenog broja koraka algoritam daje raspodelu broja veza po čvoru . To znači da raspodela broja veza po čvoru u mreži ne zavisi od veličine sistema i kako topološke karakteristike ovih mreža ne zavise od njihove veličine, ove mreže se zovu mreže bez skale. Eksponent kod ovog modela zavisi od veličine početne mreže. U ovom radu, za N₀=3 i m=2, izveden je n=61algoritamski korak. Dobijena mreža se sastoji od N=64 čvora i 𝜆=2(Slika 2.).

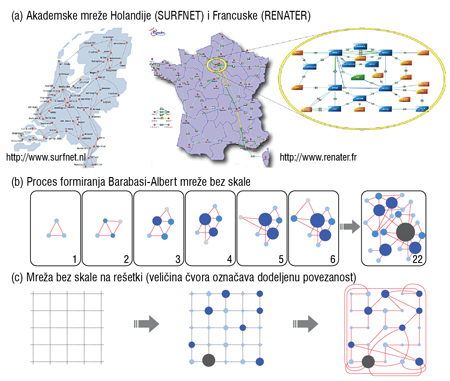
Slika 1. Šematski prikaz (a) akademskih mreža Holandije (SURFNET) i Francuske (Renater), kao i procesa formiranja mreže u generičkim modelima mreža bez skale (b) za Barabàsi-Albert model i (c) na rešetki.

Međutim, u realnosti mreže se nalaze u prostoru i ograničene su cenom realizacije veze između čvorova. U modelu mreža bez skale na rešetki (scale free on lattice, SFL), [20], algoritam koristi skup čvorova koji se nalaze na kvadratnoj rešetki dimenzija n x n. Rastojanje između dva čvora je definisano kao minimalan broj „koraka na rešetki“ kojim se dolazi od jednog čvora do drugog. U ovom modelu čvorovima mreže se nasumično dodeljuje broj linkova (k_i) koji bi trebalo da se uspostavi prema raspodeli p(k)=Ak ^{- 𝜆}, 2 < k < K. Potom se ti čvorovi nasumičnim redosledom povezuju sa svojim najbližim susedima koji u tom trenutku imaju još slobodnih veza. Važno je napomenuti da je u ovom modelu eksponent 𝜆parametar modela. Ovde koristimo vrednost 𝜆=2 koja je dobijena iz raspodele povezanosti čvorova u Nacionalnim istraživačkim i obrazovnim mrežama (NRENs) Francuske i Holandije. Izbor parametra modela 𝜆je, takođe, u skladu sa raspodelom dobijenom BA modelom. Za normalizacionu konstantu važi A ~ (𝜆-1)m^{𝜆 - 1}, za neko veliko k.

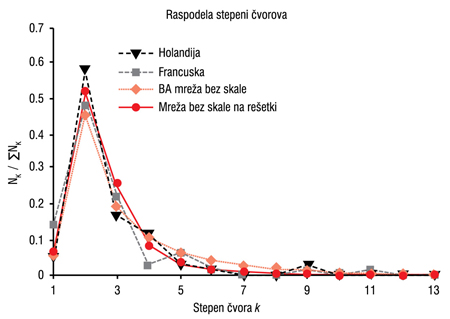
Slika 2. Raspodele povezanosti čvorova u akademskim mrežama Holandije i Francuske, kao i mreža bez skale dobijenih generičkim modelima (b) Barabàsi-Albert i (c) na rešetki.

U ovom radu posmatrali smo i dve realne mreže: nacionalne akademske mreže Holandije (NSFnet) i Francuske (Renater). Topologija Renater mreže podrazumeva mrežu u mreži, tj. Pariz se može posmatrati kao podmreža. Izabrane mreže imaju 59 (NSFnet) i 63 (Renater) čvora, tako da možemo pretpostaviti da svaka tačka u mreži ima informaciju o topologiji mreže i mogu se koristiti statički i dinamički algoritmi rutiranja. Takođe, možemo pretpostaviti da čvorovi u ovakvoj mreži razmenjuju informacije koje se mogu iskoristiti u procesu rutiranja. Na Slici 2. je prikazana raspodela povezanosti za opisane mreže. Sa Slike 2. se vidi da raspodela povezanosti čvorova, koja odgovara mrežama bez skale, važi i kod ove dve realne komunikacione mreže.

Na prvi pogled, najefikasniji način da se prenese informacija kroz mrežu je duž najkraće putanje. U praksi je često zastupljena metoda rutiranja po najkraćoj putanji, ili neki sličan način rutiranja izveden iz ovog metoda. Zato raspodela dužina najkraćih putanja u mreži pruža korisne informacije o topološkim osobinama mreže koje utiču na njene transportne karakteristike. Iz raspodele dužina putanja, moguće je uvesti i prečnik mreže kao dužinu puta između najudaljenijih čvorova mreže. Mali prečnik mreže omogućava da se paketi brzo prenose kroz mrežu duž najkraće putanje, smanjujući time mogućnost gubitaka usled zagušenja čvorova. To znači da mreže sa malim prečnikom imaju veću kritičnu vrednost protoka u odnosu na mreže sa velikim prečnikom. Obe razmatrane akademske mreže imaju prečnik mreže D=11. Barabàsi i Albert algoritam kojim je generisana mreža bez skale (BA) kao rezultat dao je mreže sa znatno manjim prečnikom D=6,84 (srednja vrednost). Prosečan prečnik mreža bez skale na rešetki (SFL) je D=10,81, i blizu je prečnika dve akademske mreže. Sa Slike 3. može se, takođe, videti da raspodela dužina najkraćih putanja u mreži bez skale (BA) ne odgovara realnim mrežama. Ovo nije iznenađujuće, jer je u ovom modelu prostorno rastojanje između čvorova irelevantno. U slučaju mreže bez skale na rešetki, raspodela dužina putanja prati raspodelu dve nacionalne akademske mreže.

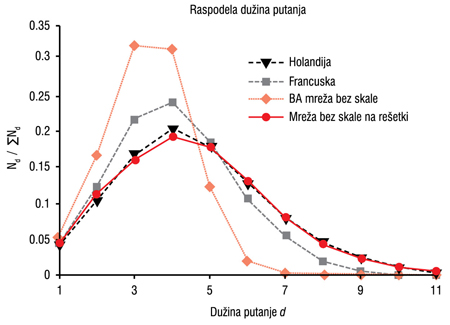
Slika 3. Raspodela dužina najkraćih putanja u akademskim mrežama Holandije i Francuske, kao i dobijenih generičkim modelima mreže bez skale (N=64, m=2, BA) i bez skale na rešetki (N=64, 𝜆=2, SFL).

Komunikacija dva čvora između kojih ne postoji direktan link, na primer, između čvorova j i k, zavisi od čvorova koji se nalaze na putanji između njih. Kao veličina koja opisuje stanje čvora koristi se statičko opterećenje, koje predstavlja ukupan broj putanja koji prolazi kroz taj čvor. Statičko opterećenje čvora i se definiše kao [24, 25]

(1)

gde n_jkpredstavlja ukupan broj putanja koje povezuju čvorove j i k, dok n_jk(i) predstavlja broj putanja koje povezuju čvorove j i ki prolaze kroz čvor i. Kao što se vidi sa Slike 4, dva modela mreža bez skale imaće međusobno slične raspodele opterećenja po čvorovima. Takođe, oba modela daju raspodele statičkih opterećenja čvorova koje odgovaraju akademskim mrežama Holandije i Francuske. Prethodna istraživanja [25] pokazala su da raspodela opterećenja čvorova u mrežama bez skale, kada se posmatraju najkraće putanje, zavisi od stepena čvora b(k)~k^δ. To znači da će u mrežama bez skale (koje opisuju čitavu klasu realnih mreža) čvorovi sa većim brojem linkova biti više opterećeni, odnosno, topologija mreže će uticati na opterećenje čvorova. Važno je napomenuti da ovaj zakon važi na nivou cele i dovoljno velike mreže.

3. PROTOK INFORMACIJA - MODEL SAOBRAĆAJA U MREŽAMA

Zbog jednostavnosti, za sve čvorove u ovom radu je pretpostavljeno da su ujedno i hostovi i ruteri, tj. da mogu i da šalju i da prosleđuju podatke. Svaki čvor ima unapred definisan maksimalan kapacitet rutiranja paketa C, dok, sa druge strane, komunikacioni kanali imaju neograničen kapacitet za prenos paketa. Ako paketi stignu do čvora čiji je maksimalni kapacitet za usmeravanje (rutiranje) dostignut (tj. čvor je zagušen), biće odbačeni. Dinamika modela je sledeća: u svakom trenutku (t) u čvorovima se generišu paketi sa verovatnoćom p. Verovatnoća p predstavlja kontrolni parametar: male vrednosti parametra p odgovaraju maloj gustini paketa (saobraćaja) u mreži, dok velike vrednosti parametra ppodrazumevaju veliki broj paketa, tj. veliki saobraćaj u mreži. Podrazumeva se da svi paketi imaju jednaku dužinu i da u jednom trenutku čvor može da pošalje najviše jedan paket. Nakon generisanja paketa, na slučajan način se bira odredišni čvor u mreži ka kome će paket biti prosleđen, pri čemu se izvorišni i odredišni čvor moraju razlikovati. Vreme propagacije T se definiše kao vreme koje protekne od trenutka generisanja paketa do trenutka kada će paket biti isporučen na odredište. Ovde su zanemarena kašnjenja koja unose čvorovi i linkovi, tako da se paket prenosi u jediničnom intervalu vremena između međusobno povezanih čvorova, bez obzira na rastojanje između ta dva čvora. Znači, u vremenskim intervalima t+1, t+2, ..., t+T, paket putuje ka svom odredištu a vreme propagacije T zavisi od dužine putanje (dužina putanje je određena brojem linkova potrebnim da se paket prenese od svog izvora do odredišta). Kada paket pristigne na odredište, nestaje iz mreže.

Ukoliko je broj generisanih paketa mali, svi paketi će biti isporučeni na odredište. Obrnuto, kada je broj poslatih paketa veći od neke kritične vrednosti, dolazi do zagušenja. U toj situaciji, paket koji pristigne u zagušeni čvor biće odbačen. Prema tome, u režimu gde postoji zagušenje, broj generisanih paketa je veći od broja paketa koji su isporučeni na odredište. Broj odbačenih paketa može poslužiti kao mera kvaliteta usluge posmatranog sistema - visok broj odbačenih paketa ukazuje na loš kvalitet usluge. Verovatnoću da će poslati paket biti odbačen η, definišemo kao

(2)

odnos ukupnog broja odbačenih paketa R_d i ukupan broj generisanih paketa R. Visoka verovatnoća odbacivanja paketa pokazuje da veliki broj paketa ne može da stigne na svoje odredište i da je kvalitet usluge loš.

4. IV. METODE ZA POBOLJŠANJE PERFORMANSI

4.1. Statičko rutiranje

Za prenos podataka mogu se koristiti različite strategije rutiranja. U slučaju statičkog rutiranja dve najčešće strategije su rutiranje po najkraćoj putanji i „efikasno“ rutiranje kod koga su linkovima dodeljene cene (težine). U slučaju rutiranja kad su linkovima dodeljene cene, putanja kojom će paket biti prosleđen bira se tako da zbir cena linkova bude minimalan. Izabrana putanja upisuje se u tabelu rutiranja i svi paketi između odgovarajućeg izvora i odredišta koristite tu putanju. Kod rutiranja po najkraćoj putanji, svi linkovi imaju istu cenu. Rutiranje po najkraćim putanjama je, naravno, najefikasnije kada su u pitanju brzina i ekonomičnost, ali u situaciji kada je količina saobraćaja u mreži izuzetno velika, stepen verovatnoće da će se zagušenje pojaviti u čvorovima koji imaju veliku vrednost statičkog opterećenja je veoma visok. Jasno je da će zaobilaženjem opterećenih čvorova paket imati veće šanse da bude isporučen na odredište. Kako bismo pronašli optimalan algoritam rutiranja, možemo uvesti pojam „efikasne putanje“ [1]. Cena linka između čvorova s i tdefinisana je kao

(3)

gde je β parametar. Na Slici 4. može se posmatrati kako se menjaju vrednosti standardnog odstupanja statičkog opterećenja i srednje dužine putanja kada se paketi rutiraju po putanjama koje imaju najmanje cene za različite vrednosti parametra β. Standardno odstupanje statičkog opterećenja je minimalno kada je opterećenje ravnomerno raspoređeno po svim čvorovima mreže. Zato optimalna vrednost parametra β odgovara poziciji minimuma standardnog odstupanja opterećenja, tj. β=1±0,1. Ovo je takođe optimalna vrednost za akademsku mrežu Holandije. Optimalna vrednost za francusku akademsku mrežu je veća, odnosno β=1,2±0,1, zbog većeg odstupanja. Ipak, odabir putanja koje nisu najkraće izaziva blag porast srednje dužine puta paketa.

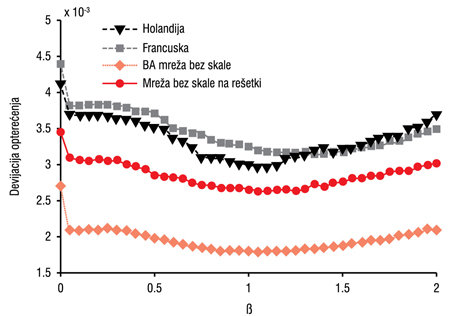
Slika 4. Standardno odstupanje vrednosti statičkog opterećenja u funkciji od parametra β za različite modele mreža.

4.2. Dinamičko rutiranje

U ovom radu smo analizirali efikasnost dinamičkog rutiranja produžavanjem putanje u slučaju kada je čvor na koji paket nailazi zagušen. Ova strategija je pogodna za mreže gde čuvanje (buffering) podataka nije moguće (npr. zbog količine ili arhitekture čvorova). Pretpostavlja se da svaki čvor zna opterećenje svojih suseda. Neka je putanja između čvorova i i j, P(i→j) := x₀,x₁,...,x_n, gde je x₀ = i i x_n = j. Nakon određivanja putanja, raspodela statičkog opterećenja u mreži neće biti uniformna i do zagušenja će dolaziti u čvorovima sa većom vrednošću statičkog opterećenja. Pošto zagušenja u čvorovima nisu stalna čak ni za protoke bliske kritičnom, broj odbačenih paketa može se smanjiti tako što će se putanje koje prolaze kroz opterećene čvorove produžiti, ukoliko su zadovoljeni određeni uslovi. Ideja je da se paketi, umesto da se pošalju ka zagušenim čvorovima, vrate jedan korak unazad. To znači sledeće: ukoliko čvor x_m u trenutku t primi signal o zagušenju čvora x_m+1, vratiće paket čvoru x_m-1, ukoliko je ovaj čvor slobodan da primi paket. Zatim će u trenutku t+1, čvor x_m-1 poslati ponovo paket ka čvoru x_m. Da bi se izbeglo smanjenje performansi sistema, za svaki čvor i definisan je parametar q_i=b_iNp tako da čvor može vratiti paket jedan korak unazad ukoliko je zadovoljen uslov q_i<0,5C. Ovde posmatramo scenario kada 10% čvorova sa najvećom vrednošću statičkog opterećenja ima mogućnost slanja upozorenja o zagušenju svojim susedima. Veći broj čvorova ne donosi značajnije poboljšanje.

4.3. Simulacije saobraćaja u mrežama

Da bi se ocenilo poboljšanje dobijeno različitim strategijama rutiranja, algoritmi rutiranja su primenjeni na dve generičke mreže, kao i na akademske mreže Holandije i Francuske i izračunata je zavisnost verovatnoće gubitka paketa η od broja generisanih paketa. Na Slici 5. su prikazane vrednosti η za različite verovatnoće generisanja paketa p kada se paketi prosleđuju po najkraćim putanjama. U konkretnim realnim mrežama, kao i u modelu mreže bez skale na rešetki za vrednosti p > 0,1 više od 40% paketa biće odbačeno ukoliko je kapacitet rutiranja čvorova C = 2, dok u mrežama kod kojih je kapacitet rutiranja C = 4, broj odbačenih paketa počinje ubrzano da se povećava. Rezultati simulacija pokazali su da je zagušenje najmanje u BA mrežama, što je u skladu sa činjenicom da ove mreže imaju manju prosečnu dužinu putanja.

Poboljšanje ostvareno statičkim i dinamičkim strategijama rutiranja prikazano je na Slikama 6. i 7, respektivno. Pomoću rutiranja po efikasnim putanjama može se značajno smanjiti zagušenje u posmatranim mrežama. Kada je količina generisanog saobraćaja u mreži mala i srednja (p < 0,3), opterećenje čvorova koji imaju veliko statičko opterećenje je preraspodeljeno na ostale čvorove, pa se performanse mreže popravljaju za 30% - 80%. Za iste vrednosti p dinamičko rutiranje ostvaruje manja poboljšanja (oko 10%), osim u slučaju BA mreže. Za velike vrednosti verovatnoće, p > 0,3, u celom sistemu se javlja zagušenje i efekat optimizacije se smanjuje. Pri tome, rutiranjem po efikasnim putanjama ostvareno je veće poboljšanje performansi u SFL mreži i nacionalnim mrežama Holandije i Francuske u odnosu na BA mrežu, i to zahvaljujući većem prečniku ovih mreža koji omogućava veći saobraćaj u njima za istu vrednost parametra p.

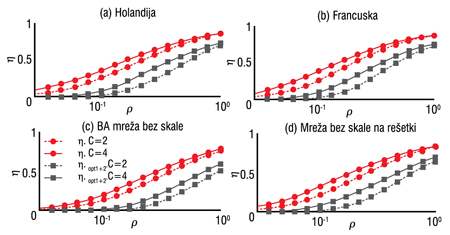
Slika 5. Poređenje performansi mreža kada se koristi statičko rutiranje po najkraćim putanjama (η) i kada se koristi kombinovano dinamičko i statičko rutiranje (η_opt1+2).

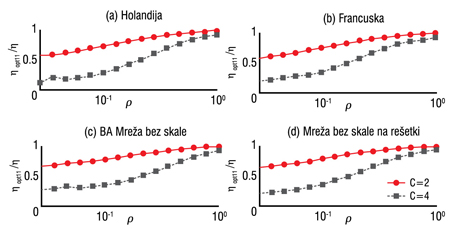
Slika 6. Poboljšanjeperformansi mreža kada se koristi rutiranje po najkraćim putanjama (η) i kada se koristi rutiranje po efikasnim putanjama (η_opt1).

Dinamičko i statičko rutiranje su komplementarne strategije i moguće ih je kombinovati da bi se postigao bolji kvalitet servisa. Na Slici 5. prikazani su gubici pre (rutiranje po najkraćim putanjama) i posle primene dinamičkog i statičkog rutiranja. Preraspodela opterećenja sa čvorova sa velikim brojem veza (i samim tim velikim statičkim opterećenjem) omogućava efikasnije rutiranje dinamičkim produžavanjem putanje. Sa Slike 5. se jasno vidi da optimizacija unosi značajno poboljšanje, osim kada u mreži postoji izuzetno veliko zagušenje (p > 0,9). U realnim situacijama (p ~ 0,05 – 0,7), mogu se značajno smanjiti gubici u prenosu podataka u mreži, a samim tim i popraviti kvalitet usluge. Generička SFL mreža i akademska mreža Francuske pokazuju posebno veliko poboljšanje zbog udaljenosti najopterećenijih čvorova. Nasuprot tome, u holandskoj mreži četiri najopterećenija čvora i pre i posle optimizacije ostali su u blizini (iako su se sami čvorovi promenili).

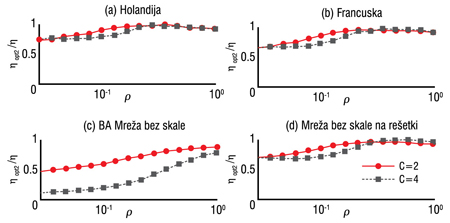
Slika 7. Poboljšanjeperformansi mreža kada se koristi statičko rutiranje po najkraćim putanjama (η) i kada se koristi dinamički modifikovano rutiranje po najkraćim putanjama sa vraćanjem paketa (η_opt2).

5. ZAKLJUČAK

U ovom radu predstavljena su dva modela kompleksnih mreža bez skale, i prikazane su neke od njihovih osobina koje imaju bitnu ulogu u procesu prenosa informacija. Za poređenje su odabrane dve realne mreže: nacionalne akademske mreže u Holandiji i Francuskoj. Ove dve mreže imaju sličan broj čvorova (59, odnosno 63), a i njihove topološke karakteristike, kao što su raspodela stepeni čvorova, dužine putanja i raspodela statičkog opterećenja čvorova, su jako slične. Poređenje ovih karakteristika sa mrežama bez skale pokazalo je da generički modeli mreža bez skale na rešetki najbolje modeluje karakteristike izabranih realnih mreža. U nastavku rada, analizirana je dinamika procesa prenosa informacija (u obliku paketa) i strategije kojima se performanse ovih mreža mogu poboljšati bez promene njihove topologije. Analiziran je model saobraćaja koji podrazumeva da čvorovi u mreži imaju ograničene kapacitete procesiranja podataka i nemaju bafere u kojima bi se čuvali paketi kada dođe do zagušenja. Kako su izabrane relativno male mreže, kašnjenje u mreži nije kritično, pa meru kvaliteta servisa predstavlja broj odbačenih paketa. Upoređene su dve strategije, rutiranje po efikasnim putanjama i rutiranje sa vraćanjem paketa. Rutiranje po efikasnim putanjama predstavlja statičko rešenje, gde je svakom linku pridružena cena proporcionalna opterećenju čvorova. Ovom strategijom se postiže da se saobraćaj, koji bi prolazio kroz najopterećenije čvorove, preraspodeli po ostalim, manje opterećenim čvorovima. Pošto je uočeno da se zagušenje najčešće javlja u čvorovima sa velikim statičkim opterećenjem i da do zagušenja dolazi u diskretnim vremenskim intervalima, predloženo je rutiranje sa vraćanjem paketa kojim bi trebalo da se izbegne zagušenje u tim čvorovima. Rezultati simulacija pokazali su da verovatnoća gubitka paketa može značajno da se smanji kombinacijom rutiranja po najkraćim putanjama i rutiranja sa vraćanjem paketa, odnosno ravnomernijom raspodelom opterećenja i izbegavanjem kritičnih situacija kada postoji zagušenje u određenim čvorovima.

Autori se zahvaljuju podršci Ministarstva za prosvetu i nauku Republike Srbije, kroz projekt br. ON171017. Autori takođe zahvaljuju na podršci koju su dobili kroz SCOPES projekt IZ73Z0–128169 švajcarske Nacionalne fondacije za nauku.

Slika 8. PARADOX superračunar.

Za numeričke simulacije korišćen je PARADOX klaster-superračunar smešten u Laboratoriji za primenu računara u nauci na Institutu za fiziku u Beogradu. Resursi PARADOX-a se sastoje od 89 radnih i 15 servisnih jedinica, odnosno 704 procesora i 50 terabajta skladišnog prostora. Zahvaljujući tome istraživači imaju na raspolaganju 1,2 miliona časova, ili 137 godina, procesorskog vremena svakog meseca. Radne jedinice su međusobno povezane gigabitnim eternetom u topologiju zvezde. Servisne jedinice obezbeđuju rad centralnih Grid servisa nacionalne mreže, kao i celokupno administriranje virtuelnih zajednica korisnika. Predstojećom nadogradnjom PARADOX klastera, trenutna performansa od 6 TFlop-a biće uvećana do 40 TFlop-a. PARADOX klaster predstavlja okosnicu super-računarske infrastrukture jugoistočne Evrope i deo je šire AEGIS e-infrastrukture, koja je delom finansirana kroz projekte Okvirnog programa 7 Evropske unije EGI-InSPIRE, PRACE-1IP i HP-SEE.

Literatura

[1] G. Yan, T. Zhou, B. Hu, Z.-Q. Fu, and B.-H. Wang, Phys. Rev.E 73, 046108 (2006).

[2] M. Tang and T. Zhou, Phys. Rev. E 84, 026116 (2011).

[3] B. Danila, Y. Sun, and K. E. Bassler, Phys. Rev. E 80, 066116 (2009).

[4] B. Danila, Y. Yu, J. A. Marsh, and K. E. Bassler, Phys. Rev. E 74, 046106 (2006).

[5] R. Guimerà, A. Arenas, A. Díaz-Guilera, F. Giralt, Phys. Rev. E 66, 026704 (2002).

[6] W.-X. Wang, B.-H. Wang, C.-Y. Yin, Y.-B. Xie, and T. Zhou, Phys. Rev. E 73, 026111 (2006).

[7] C.-Y. Yin, B.-H. Wang, W.-X. Wang, T. Zhou, and H.-J. Yang, Phys. Lett. A 351, 220 (2006).

[8] S. Sreenivasan, R. Cohen, E. Lopez, Z. Toroczkai, and H. E. Stanley, Phys. Rev. E 75, 036105 (2007).

[9] W.-X. Wang, C.-Y. Yin, G. Yan, and B.-H. Wang, Phys. Rev. E 74, 016101 (2006).

[10] B. Kujawski, G. J. Rodgers, and B. Tadić, Lect. Notes Comput.Sci. 3993, 1024 (2006).

[11] P. Echenique, J. Gómez-Gardeñes, and Y. Moreno, Phys. Rev. E 70, 056105 (2004).

[12] P. Echenique, J. Gómez- Gardeñes, and Y. Moreno, Europhys.Lett. 71, 325 (2005).

[13] X. Ling, M.-B. Hu, R. Jiang, and Q.-S. Wu, Phys. Rev. E 81, 016113 (2010).

[14] D.-H. Kim and A. E. Motter, J. Phys. A: Math. Theor. 41, 224019 (2008).

[15] D.-H. Kim and A. E. Motter, New J. Phys. 10, 053022 (2008).

[16] E. W. Dijkstra, Numer. Math. 1, 269 (1959).

[17] E. W. M. Wong, L. L. H. Andrew, T. Cui, B. Moran, A. Zalesky, R. S. Tucker, M. Zukerman, J. Lightwave Technol.

27(14):2817-2833 (2009).

[18] S.N. Dorogovtesev, J.F.F. Mendes, Evolution of Networks, Oxford University Press, Oxford, 2003.

[19] A.-L. Barabási, R. Albert, Science 286, 509 (1999).

[20] A.F. Rozenfeld, R. Cohen, D. ben-Avraham, S. Havlin, Phys. Rev. Lett. 89, 218701 (2002).

[21] G. Caldarelli, Scale-free networks, Oxford Univ. Press, Oxford, 2007.

[22] http://www.renater.fr.

[23] http://www.surfnet.nl.

[24] P. Holme and B.J. Kim, Phys. Rev. E 65, 066109 (2002).

[25] K.-I. Goh, B. Kahng, and D. Kim, Phys. Rev. Lett. 87, 278701 (2001).

Autori

Jelena Smiljanić (1987) diplomirala je 2011. na Elektrotehničkom fakultetu u Beogradu. Od 2010. je angažovana na projektima u Institutu za fiziku u Beogradu u Laboratoriji za primenu računara u nauci, prvo kao student saradnik, a potom kao istraživač pripravnik. Bavi se problemima transporta i rutiranja informacije u telekomunikacionim mrežama.

Milan Žeželj (1985) diplomirao je 2009. na Elektrotehničkom fakultetu u Beogradu. Od 2009. je angažovan na projektima u Institutu za fiziku u Beogradu u Laboratoriji za primenu računara kao istraživač saradnik. Bavi se problemima perkolacije i električnog transporta u mrežama karbonskih nanotuba i nanožica. Autor je dva rada u časopisima sa SCI liste.

Igor Stanković (1976) diplomirao je 1999. na Elektrotehničkom fakultetu u Beogradu, i doktorirao je 2004. na Tehničkom univerzitetu u Berlinu. Bavi se problemima transporta u kompleksnim strukturama. Od 2005. do 2009. bio je inženjer za simulacije kompanije Tojota motor Evropa u Briselu. Od 2009. je naučni saradnik na Institutu za fiziku u Beogradu u Laboratoriji za primenu računara u nauci. Autor je jednog međunarodnog patenta i 9 radova u časopisima sa SCI liste. Od 2009. do 2012. bio je savetnik na projektu Evropske mreže preduzetništva. Od 2009. vodi udruženi istraživački projekat sa švajcarskim Federalnim institutom za tehnologiju iz Ciriha (ETH Zürich).