CASOPIS REPUBLICKE AGENCIJE ZA TELEKOMUNIKACIJE

SADRŽAJ

Rad se bavi razmatranjem numeričke karakterizacije elektromagnetske sprege putem otvora u oklopljenim kućištima pri čemu su analizirani pojedinačni otvori koji se koriste za pristup elektronskom sistemu unutar kućišta (konektori, napajački/odvodni kablovi, CD/DVD ROM-ovi i dr.) i grupe većeg broja otvora istog oblika (npr. ventilacioni otvori) koji su namenjeni za odvođenje viška toplote iz sistema. Za potrebe modelovanja korišćen je TLM solver koji se duži niz godina razvija u okviru Laboratorije za mikrotalasnu i submilimetarsku tehniku i bežične komunikacije na Elektronskom fakultetu u Nišu, kao i jedan komercijalni softverski paket, takođe na bazi TLM metoda. Za potrebe analize pojedinačnih otvora primenjen je konvencionalni pristup u vidu numeričke mreže velike rezolucije, dok je za ventilacione otvore korišćen tzv. integralni pristup baziran na odgovarajućem kompaktnom modelu. Na nekoliko karakterističnih EMC primera, ilustrovani su efekti prisustva otvora, njihovog broja i međusobne blizine, kao i debljine metalnih zidova u kojima se otvori nalaze, na karakteristike oklopa.

1. UVOD

U današnje vreme digitalni i analogni elektronski sistemi postaju sve složeniji i samim tim osetljiviji na brojne elektromagnetske (EM) smetnje. Takođe, broj izvora EM poremećaja u spoljašnjem okruženju je u stalnom porastu. Stoga je elektromagnetska kompatibilnost (electromagnetic compatibility – EMC) opreme, koja istovremeno odražava njenu otpornost na određeni nivo smetnji iz spoljašnje sredine i emitovanje prihvatljivog nivoa EM zračenja, od suštinskog značaja za projektovanje i rad elektronskih sistema u realnom vremenu [1]. Danas postoje brojne numeričke simulacione tehnike koje značajno olakšavaju proces projektovanja elektronske opreme u cilju ispunjavanja važećih EMC standarda. Ove tehnike omogućavaju procenu stepena sprege i interferencije između sistema i podsistema i ukazuju na optimalnu strategiju u dizajniranju opreme sa tačke gledišta EMC-a pre početka izrade prototipa.

Diferencijalne numeričke tehnike u vremenskom domenu, kao što su metod konačnih razlika (Finite-Difference Time Domain - FDTD) [2] i metod modelovanja pomoću električnih vodova (Transmission Line Matrix - TLM) [3], zahvaljujući svojim karakteristikama, našle su široku primenu u rešavanju brojnih EMC problema. Primena ove klase numeričkih metoda za analizu praktičnih EMC problema zahteva detaljno opisivanje geometrijskih i EM karakteristika problema u prostornom domenu, numeričku simulaciju njihovog odziva na realnu pobudu u vremenskom domenu i proračun odgovarajućih parametara u frekvencijskom opsegu od interesa. Pri tome se, za veliku većinu EMC problema, kao osnovni zahtev ovim metodama nameće adekvatno numeričko modelovanje uzajamne interakcije pobudnog EM polja i geometrijski malih, ali u električnom smislu važnih struktura (tanke žičane strukture i složeni žičani spojevi, prorezi, otvori i sl.), umetnutih unutar fizički velikih i oklopljenih sistema.

Konvencionalni pristup u modelovanju ovakvih struktura zasniva se na primeni numeričke mreže veće rezolucije (odnosno čvorova malih dimenzija), kako bi se tačno opisalo njihovo EM prisustvo. Preostali deo sistema obično se opisuje mrežom dimenzionisanom za modelovanje prostiranje EM talasa u slobodnom prostoru. Ovaj pristup, koji sa razvojem moćnih računarskih stanica postaje generalno primenljiv čak i na električno male strukture (strukture čije su dimenzije značajno manje od talasne dužine od interesa za EMC analizu), ipak u nekim slučajevima rezultira u neprihvatljivo velikom broju čvorova i velikom trajanju simulacije. Stoga su danas aktuelna istraživanja koja imaju za cilj poboljšanje ovih numeričkih tehnika u cilju efikasnije simulacije brojnih praktičnih višedimenzionalnih EMC problema. Kada je reč o TLM metodu, do sada je za potrebe efikasnijeg modelovanja žičanih struktura [4], proreza [5] i ventilacionih otvora [6] razvijeno nekoliko kompaktnih modela, implementiranih lokalno unutar jednog ili više čvorova (tzv. integralni pristup). U poređenju sa konvencionalnim pristupom, ovi modeli obezbedili su značajne uštede računarskih resursa potrebnih za numeričko rešavanje EMC problema.

U pogledu EMC-a, osim od karaktera pobudnog EM zračenja i konfiguracije žičanih i dielektričnih struktura unutar sistema, performanse elektronskih sistema dominantno zavise od postojanja i prirode sprežnih puteva preko kojih se ostvaruje sprega EM energije izvora i osetljivih elektronskih sistema. Glavnu ulogu pri eliminisanju ili redukovanju ovih sprežnih puteva imaju oklopljena kućišta. Ova kućišta, napravljena od provodnih materijala odgovarajuće debljine i sa različitim EM karakteristikama, utiču na nivo EM zračenja koje dopire do električnog kola iz spoljašnje sredine, ali takođe i određuju koliko se energije od strane kola izrači u spoljašnju sredinu. Kako oklopi neizbežno poseduju pojedinačne otvore koji se obično koriste za pristup sistemu (konektori, napojni/odvodni kablovi, CD/DVD ROM-vi i dr.) i/ili više otvora istog oblika za hlađenje i odvođenje viška toplote iz sistema (npr. ventilacioni otvori), EM zračenje preko otvora prodire u prostor unutar i izvan oklopa, degradirajući osnovnu funkciju oklopljavanja. Pored ovog načina sprege, moguće je izdvojiti i spregu putem difuzije kroz nesavršeno provodne zidove oklopa. Ukoliko se pretpostavi da je provodnost zidova oklopa jako velika, EM sprega putem otvora dominantno utiče na rad elektronskih sistema sa tačke gledišta EMC-a, budući da otvori svojim prisustvom mogu značajno povećati nivo EM emisije kroz oklop.

Kako bi se izvršila adekvatna karakterizacija količine EM energije koja putem otvora prodire u prostor unutar i van oklopa i procenila efikasnost oklapanja, u ovom radu je primenjen TLM numerički metod implementiran kroz odgovarajuće softverske pakete. U nastavku su razmatrani kako pojedinačni tako i ventilacioni otvori sa oblicima (pravougaoni, kružni i kvadratni) koji se najčešće sreću u oklopljenim kućištima. Za modelovanje pojedinačnih otvora (jedan ili dva otvora) korišćen je komercijalni TLM softverski paket CST MICROSTRIPES™, kako bi se konvencionalnim pristupom baziranim na primeni TLM mreže velike rezolucije (naročito u prostoru unutar i oko otvora) adekvatno opisalo EM prisustvo otvora. U slučaju ventilacionih otvora, ovaj pristup čini njihovu računarsku simulaciju veoma zahtevnom u pogledu memorije i dužine simulacije, budući da svaki ventilacioni otvor treba adekvatno opisati. Stoga je primenjen drugi, tzv. integralni pristup, koji koristi kompaktni TLM model za ventilacione otvore na metalnim zidovima. Ovaj model, razvijen u [6] za kvadratne i kružne otvore, a zatim proširen i na pravougaone otvore [7], implementiran je u 3D TLMscn solver koji se duži niz godina razvija u okviru naučno-istraživačke Laboratorije za mikrotalasnu i submilimetarsku tehniku i bežične komunikacije na Elektronskom fakultetu u Nišu. Ovaj TLM simulator je prethodno uspešno primenjen za modelovanje brojnih složenih mikrotalasnih struktura, npr. realnih mikrotalasnih aplikatora na bazi cilindričnih rezonatora datih u referencama [8,9]. U ovom radu je na nekoliko karakterističnih primera izvršena ilustracija uticaja otvora, njihove brojnosti i međusobne sprege, kao i debljine zidova u kojima se ovi otvori nalaze, na karakteristike oklopljenih kućišta sa tačke gledišta EMC-a.

2. MODELOVANJE OTVORA

2.1. TLM modelovanje pojedinačnih otvora

Kada se govori o konvencionalnom modelovanju oklopljenih metalnih kućišta sa pojedinačnim otvorima, primenom TLM numeričke tehnike u vremenskom domenu, mogu se izdvojiti dve grupe problema: električno mali otvori (otvori čije dimenzije su značajno manje u poređenju sa talasnom dužinom od interesa za EMC analizu) i električno veliki otvori. Opisivanje električno velikih otvora obično ne zahteva mrežu sa rezolucijom značajno većom od one kojom se opisuju druge strukture u sistemu, pa stoga ne dovodi do povećanja potrebne memorije i brzine procesora za EMC simulaciju.

Za razliku od njih, TLM modelovanje električno malih otvora obično iziskuje nekoliko čvorova duž svake poprečne dimenzije otvora, kao i nekoliko čvorova za modelovanje debljine metalnih zidova oklopa u prostoru unutar otvora. Ovaj način omogućava da se sa dovoljnom tačnošću opišu jako izražene promene EM polja unutar i oko otvora, i to naročito na frekvencijama gde zračenje kroz ove otvore može da bude dominantno. Kako su dimenzije ovih čvorova značajno manje u odnosu na primenjenu rezoluciju u ostalim delovima mreže, ovaj pristup može da rezultira u velikom broju potrebnih čvorova u numeričkoj mreži i vrlo malom vremenskom koraku, odnosno velikoj dužini trajanja EMC simulacije u vremenu.

2.2. TLM modelovanje ventilacionih otvora

Za digitalna kola velikih brzina, oklopljena metalna kućišta koja ih okružuju obično poseduju više manjih otvora koji se koriste za ventilaciju i odvođenje toplote. Međutim, u isto vreme ovi ventilacioni otvori mogu značajno povećati zračenje i smanjiti efikasnost oklopa. Usled postojanja otvorenog prostora neophodnog za odvođenje toplote, kao i tehnoloških ograničenja u realizaciji otvora, postoji donja granica minimalne dimenzije otvora u metalnim zidovima oklopa. EM zračenje koje prodire kroz ovakve metalne zidove sa velikim brojem otvora nezanemarljivih dimenzija rezultira u pojavi smetnji, naročito na visokim frekvencijama, tj. frekvencijama iznad osnovne rezonantne frekvencije oklopa, čak i kada su u pitanju električno mali otvori.

Modelovanje ventilacionih otvora konvencionalnim TLM metodom zahteva isti pristup kao i kada su u pitanju pojedinačni otvori: veći broj čvorova za modelovanje geometrije otvora, debljine metalnih zidova i prostora u neposrednoj blizini otvora, kako bi se sa dovoljnom tačnošću opisale jako izražene promene EM polja unutar i oko otvora. Međutim, budući da je u ovom slučaju broj otvora značajno veći, računarska simulacija metalnih zidova sa ventilacionim otvorima postaje teško izvodljiva čak i sa korišćenjem moćnih računarskih stanica. Stoga je bolje primeniti integralni TLM pristup baziran na definisanju kompaktnog TLM modela za metalne zidove sa ventilacionim otvorima. Ovaj model realizovan je na interfejsu dva čvora preko ekvivalentnog kola sa induktivnim i kapacitivnim stab elementima (Slika 1.), empirijski izvedenim za otvore kružnog i kvadratnog poprečnog preseka [6], kao i pravougaone otvore [7]. Vrlo je jednostavan za implementaciju i zahteva značajno manje memorijskih resursa, budući da omogućava da se EM prisustvo ventilacionih otvora uzme u obzir koristeći čvorove čije su dimenzije značajno veće od dimenzija otvora. Pored toga, kompaktni TLM model omogućava korektno modelovanje otvora i u metalnim zidovima značajne debljine (do reda veličine dimenzija otvora). Takođe treba istaći da je model generalno primenljiv za frekvencije znatno ispod granične frekvencije otvora, kao i za frekvencije na kojima je međusobno rastojanje ventilacionih otvora manje od polovine talasne dužine, pod uslovom da se iza ventilacionih otvora ne nalaze nikakve druge strukture.

3. NUMERIČKA ANALIZA

U okviru ove sekcije predstavljeni su i analizirani rezultati dobijeni konvencionalnim i integralnim TLM pristupom za karakteristike oklopljenih metalnih kućišta sa pojedinačnim pravougaonim i kružnim otvorima i ventilacionim otvorima kvadratnog poprečnog preseka. Uloga oklopljenog kućišta je da, zavisno od frekvencije, debljine i EM karakteristika materijala od kojih je izrađeno, redukuje količinu EM energije koja prodire na prethodno opisane načine u prostor unutar i izvan oklopa i obično se izražava preko veličine koja se naziva efikasnost oklopa (shielding effectiveness - SE). Ova veličina se najčešće definiše kao odnos u dB između nivoa incidentnog polja u odgovarajućoj tački unutar sistema bez prisustva oklopa i u prisustvu oklopa, a može se definisati kako za električno (tzv. električna efikasnost) tako i za magnetsko polje (tzv. magnetska efikasnost) [1].

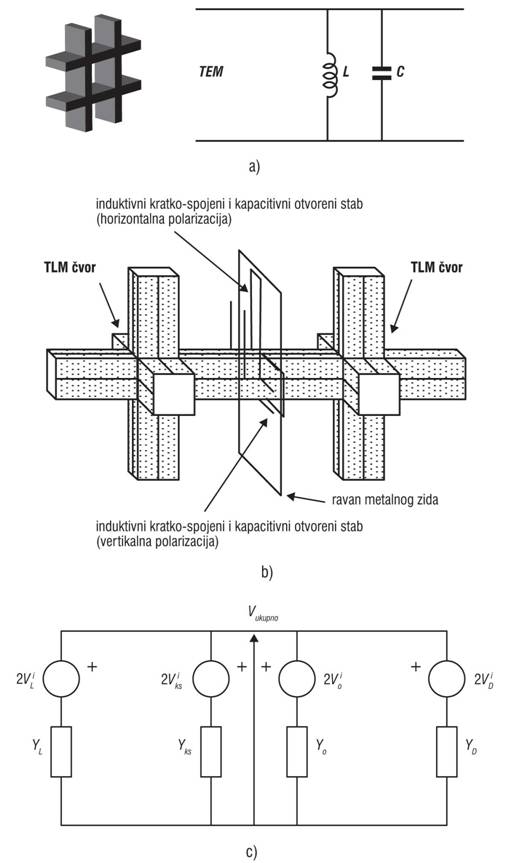
Slika 1. a) Kompaktni LC model za ventilacione otvore u metalnom zidu, b) njegova realizacija preko odgovarajućih reaktivnih stabova na interfejsu dva čvora, c) Tevenenovo (Thevenin) ekvivalentno kolo za jednu polarizaciju

U ovom radu najpre je proračunata električna efikasnost oklopa pravougaonog poprečnog preseka dimenzija: a=300 mm, b=120 mm i d=300 mm, sa jednim otvorom (Slika 2.). Debljina savršeno provodnih metalnih zidova je t=0.5 mm. Korišćena je pobuda u obliku ravanskog talasa čiji je pravac prostiranja normalan na ravan prednjeg zida sa otvorom čiji je centar u tački (a/2, b/2). Za pravougaoni otvor dimenzija l*2s = 100 mm*5 mm, odnosno kružni otvor prečnika 2r = 20 mm, električna efikasnost oklopa proračunata konvencionalnim TLM pristupom u centru oklopa prikazana je na Slikama 3. i 4. U odgovarajućim ravnima primenjeni su električni i magnetski zid kako bi se zbog simetrije problema redukovala potrebna numerička mreža. Sa slika se može uočiti odlično slaganje numeričkih TLM rezultata za električnu efikasnost oklopa sa rezultatima dobijenim analitičkim postupkom koji je razvijen u frekvencijskom domenu na bazi ekvivalentnog kola za oklop sa jednim otvorom [10].

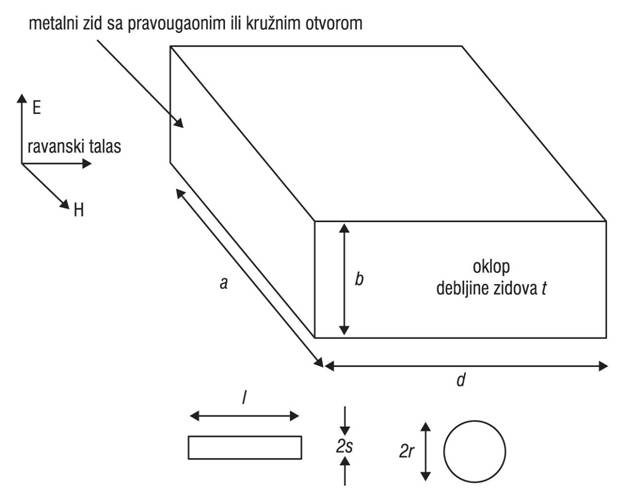
Slika 2. Oklopljeno kućište sa jednim pravougaonim ili kružnim otvorom postavljenim u centru prednjeg zida .

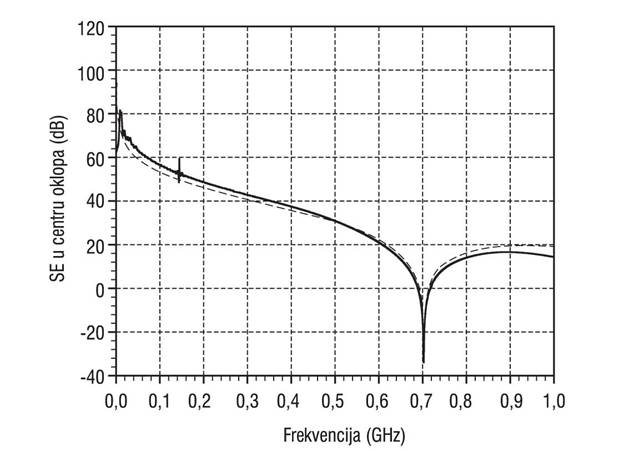
Slika 3. SE oklopa sa jednim pravougaonim otvorom proračunata u centru oklopa koristeći: a) konvencionalni TLM pristup (puna linija), b) analitički postupak opisan u referenci [10] (isprekidana linija)

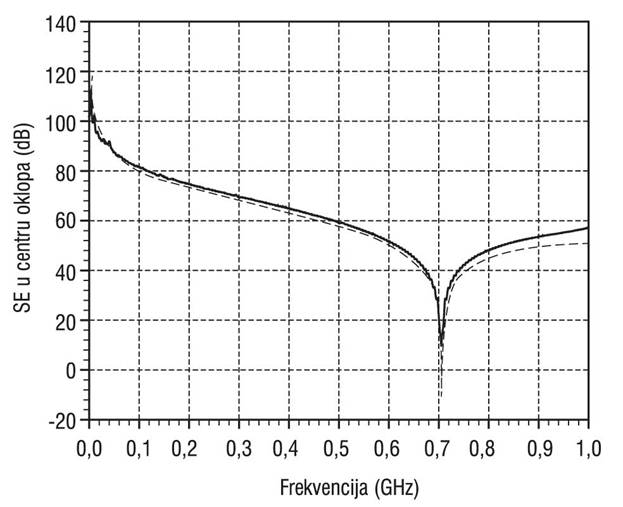
Slika 4. SE oklopa sa jednim kružnim otvorom proračunata u centru oklopa koristeći: a) konvencionalni TLM pristup (puna linija), b) analitički postupak opisan u referenci [10] (isprekidana linija)

Efekat povećanja debljine prednjeg metalnog zida koji sadrži otvor na električnu efikasnost oklopa razmatran je na primeru kućišta sa Slike 2. sa kružnim otvorom u centru prednjeg zida i ilustrovan je na Slici 5. Debljina metalnog zida povećavana je u koracima od po 0,5 mm do maksimalno 4,5 mm. Može se uočiti da se sa povećanjem debljine zidova kriva električne efikasnosti pomera ka većim vrednostima, zadržavajući pri tome svoj oblik što ukazuje na to da razmatrane debljine zidova samo utiču na slabljenje pobudnog polja prilikom prostiranja kroz unutrašnjost otvora. U frekvencijskom opsegu do 1 GHz, prisutna je samo fundamentalna rezonantna frekvencija oklopa. Sličan efekat je dobijen i za slučaj oklopa sa pravougaonim otvorom.

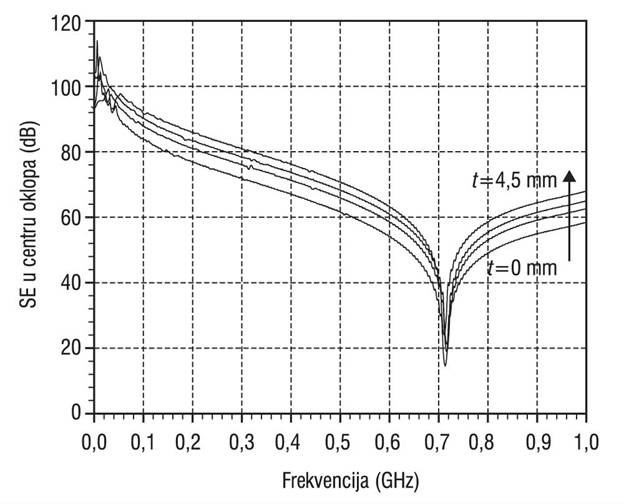
Slika 5. SE oklopa sa jednim kružnim otvorom proračunata u centru oklopa za različite debljine metalnog zida primenom konvencionalnog TLM pristupa

Efekat međusobne sprege dva pojedinačna otvora ilustrovan je na primeru oklopljenog kućišta (Slika 2.), debljine zidova t=1,5 mm. Razmatrana su dva pojedinačna kružna otvora, svaki prečnika 2r = 20 mm, postavljena simetrično u odnosu na centar metalnog zida i na međusobnom rastojanju od 30 mm odnosno 20 mm, kao i jedan veći kružni otvor postavljen u centru zida, čiji je prečnik izabran tako da površina prednjeg metalnog zida pod otvorima bude ista u oba slučaja (). Na Slici 6. prikazana je električna efikasnost u centru oklopa proračunata primenom konvencionalnog TLM pristupa. Uočava se da se, kad je međusobno rastojanje veće od njihovog prečnika, ova dva otvora ponašaju nezavisno, a električna efikasnost oklopa je ista kao u slučaju zida sa jednim većim otvorom. Do sprege između otvora dolazi na međusobnom rastojanju koje je jednako njihovom prečniku i manifestuje se u dodatnom piku koji se javlja pored fundamentalne rezonantne frekvencija oklopa. Ovo je u skladu sa zaključkom datim u referenci [11] u kome se kaže da se sprega između otvora može zanemariti u slučaju kada je njihovo međusobno rastojanje veće od veličine otvora (ali značajno manje u poređenju sa talasnom dužinom od interesa).

Integralni TLM pristup na bazi kompaktnog modela za ventilacione otvore primenjen je za proračun električne efikasnosti metalnog oklopa pravougaonog poprečnog preseka dimenzija: a=100 mm, b=80 mm i c=15 mm (Slika 7a.). Zidovi kućišta su načinjeni od aluminijuma provodnosti σ=3,54*10⁷ S/m i debljine t=0,2 mm. Svaki zid kućišta u xz ravni poseduje grupu od 45 ventilacionih otvora kvadratnog oblika dužine stranica l=5,08 mm koji se nalaze na međusobnom rastojanju p=0,69 mm (Slika 7b.). Za slučaj pobude u vidu ravanskog talasa čiji je pravac prostiranja normalan na zidove sa ventilacionim otvorima, električna efikasnost oklopa proračunata u tački 1 sa koordinatama (50, 40, 7,5) i u tački 2 (50, 50, 10) unutar oklopa, koristeći kompaktni LC model i konvencionalni TLM pristup sa mrežom visoke rezolucije prikazana je na Slici 8. Slika 8. ilustruje odlično slaganje rezultata, s tim što treba naglasiti da je simulacija u slučaju TLM mreže visoke rezolucije trajala 7 sati u poređenju sa simulacijom od 9 min za integralni TLM pristup. Takođe, Slika 8. pokazuje da električna efikasnost zavisi od pozicije za koju se proračunava unutar oklopa.

Slika 6. SE oklopa proračunata u centru oklopa primenom konvencionalnog TLM pristup za: a) dva pojedinačna otvora prečnika 2r na rastojanju 30 mm (isprekidana linija), b) jedan veći otvor prečnika (puna linija), c) dva pojedinačna kružna otvora prečnika 2r na rastojanju 20 mm (naglašena puna linija)

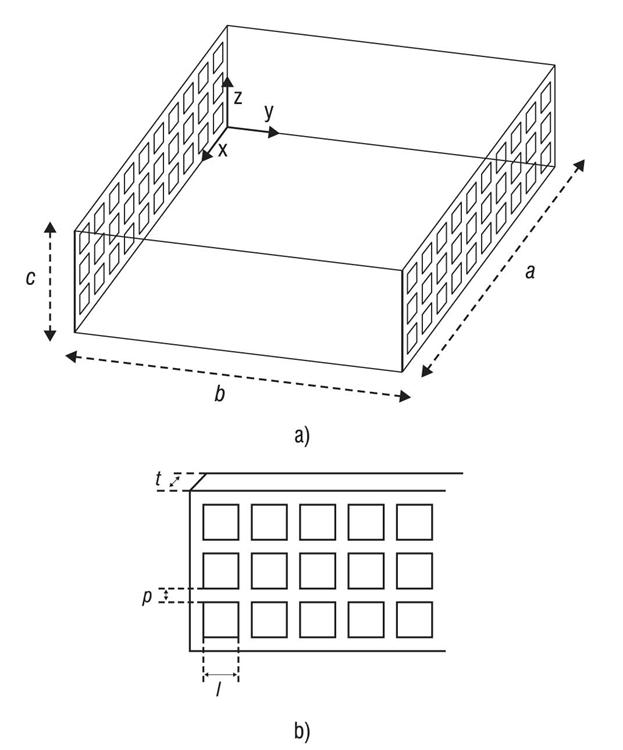
Slika 7. a) Metalni oklop pravougaonog poprečnog preseka, b) ventilacioni otvori kvadratnog oblika u metalnim zidovima u xz ravni

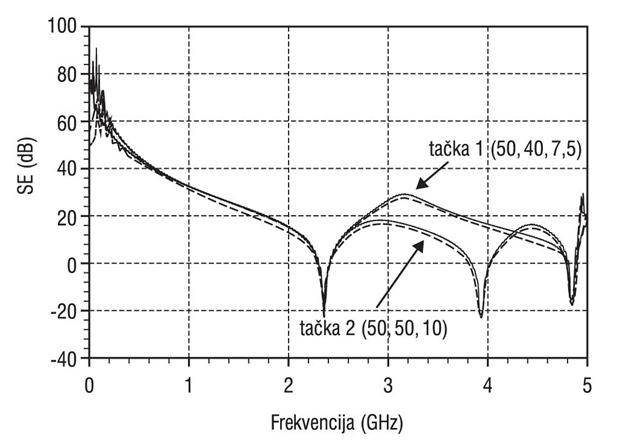
Slika 8. SE oklopa sa ventilacionim otvorima kvadratnog oblika proračunata u dvema tačkama primenom: a) kompaktnog LC modela (puna linija), b) konvencionalnog TLM pristupa (isprekidana linija)

Za većinu praktičnih EMC problema, pobuda u vidu ravanskog talasa predstavlja samo aproksimaciju realne pobude i uglavnom se koristi za proračun efikasnosti oklopa. Kada se numeričkom simulacijom procenjuje nivo EM emisije koja se izrači iz oklopljenog sistema i stepen njenog uticaja na ostale elektronske sisteme u okruženju, pobuda se smešta unutar kućišta. Jedan ovakav sistem iskorišćen je u ovom radu za ilustraciju efekta debljine zidova sa ventilacionim otvorima na nivo izračene emisije. Razmatrano je oklopljeno kućište pravougaonog poprečnog preseka dimenzija: a=50 cm, b=20 cm i c=50 cm (Slika 9.). Njegovi zidovi su načinjeni od aluminijuma provodnosti σ=3,54*10⁷ S/m. Jedan od zidova u yz ravni sadrži grupu od 252 ventilacionih otvora, kvadratnog oblika, dužine stranice l=10 mm i međusobnog rastojanja od p=5 mm.

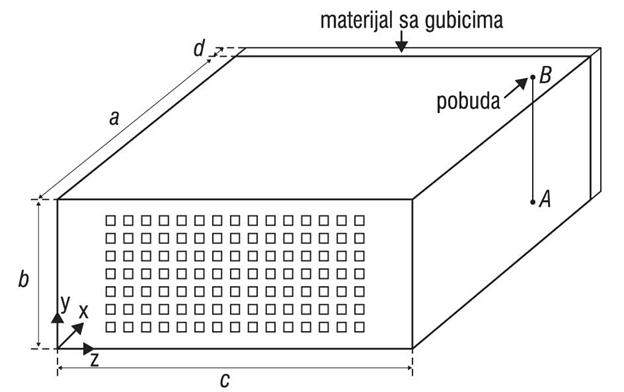
Slika 9. Oklopljeno kućište od aluminijuma pravougaonog poprečnog preseka pobuđeno dipol antenom

Kao pobuda je korišćena sonda realizovana od žice poluprečnika r=0,08 cm, čiji je položaj unutar oklopa definisan tačkama A (43 cm, 0, 33 cm) i B (43 cm, 20 cm, 33 cm). Realni naponski generator napona 1 mV i unutrašnje otpornosti 50 W postavljen je u tački B žice, dok se žica završava otpornošću od 47 W u tački A. Kako bi se redukovao faktor dobrote oklopa koji je za neopterećeni oklop neprirodno veliki, postavljen je materijal sa gubicima, provodnosti σ=2,27 S/m i debljine d=1 cm. Izbor geometrije, pobude i izlazne tačke načinjen je na osnovu eksperimentalnog kućišta korišćenog u literaturi [11].

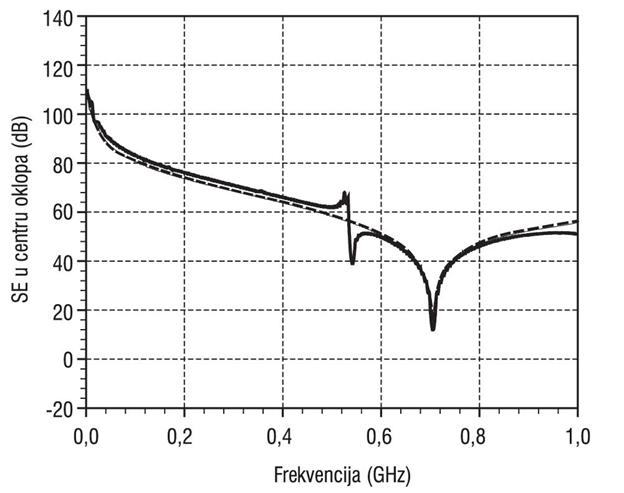
Rezultati za električno polje na rastojanju 3 m od zida kućišta sa ventilacionim otvorima, dobijeni primenom kompaktnog LC modela za dve granične debljine metalnog zida: t=0 mm i t=l=10 mm, upoređeni su sa eksperimentalnim rezultatima prezentovanim u [11] (Slika 10.). Može se uočiti odlično slaganje, izuzev na višim frekvencijama, što je posledica zanemarivanja frekvencijske zavisnosti EM karakteristika materijala sa gubicima. Takođe, efekat povećanja debljine metalnog zida koji sadrži ventilacione otvore na nivo izračenog polja sličan je kao kod pojedinačnih otvora i može se u gotovo celom frekvencijskom opsegu od interesa za analizu približno proceniti primenom empirijski procenjenog slabljenja od izvedenog u referenci [11]. Efekat međusobne sprege ventilacionih otvora uzet je u obzir pri samom definisanju kompaktnog LC modela i određen je prethodno pomenutim ograničenjima u primeni ovog modela.

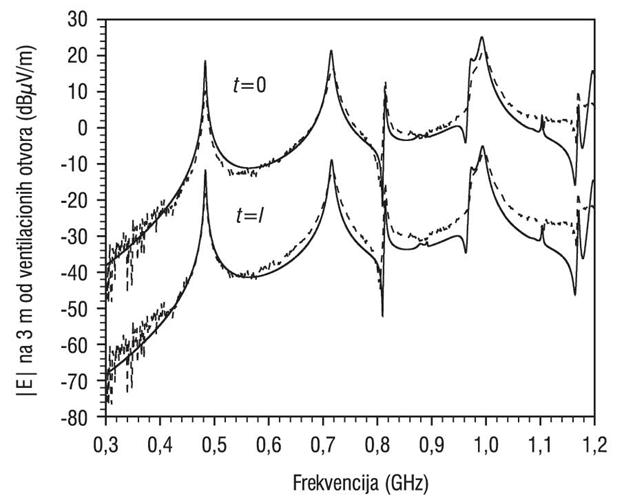
Slika 10. Električno polje na rastojanju 3 m od zida sa ventilacionim otvorima: a) kompaktni LC model (puna linija), b) eksperimentalni rezultati (isprekidana linija)

Praksa da se u cilju odvođenja viška toplote iz sistema koristi veći broj manjih ventilacionih otvora umesto manjeg broja većih otvora, kako bi se time smanjio nivo EM zračenja koji se preko otvora emituje u spoljašnju sredinu, ilustrovana je na sledeći način: analizirano je oklopljeno kućište (Slika 9.) zanemarljive debljine zidova, s tim što su pored grupe od 252 manja kvadratna otvora (dimenzija otvora je 10 mm), razmatrani i slučajevi kada je u centru zida samo jedan veći kvadratni otvor veličine 15,9 mm i grupa od 4 kvadratna otvora, svaki veličine 8 mm, simetrično raspoređenih u odnosu na centar zida. Dimenzije ovih otvora su izabrane tako da je površina metalnog zida pod otvorima približno jednaka u sva tri slučaja. Za modelovanje jednog i četiri otvora primenjen je konvencionalni TLM pristup. Na Slici 11. prikazani su rezultati za električno polje na rastojanju 3 m od zida sa otvorima. Može se uočiti da je nivo izračenog polja najveći za slučaj samo jednog otvora, a najmanji za grupu od 252 mala otvora.

Slika 11. Električno polje na rastojanju 3 m od zida sa: a) 252 manja otvora (naglašena puna linija) – kompaktni LC model, b) jednim otvorom (isprekidana linija) i c) četiri otvora (puna linija) – konvencionalni TLM pristup

4. ZAKLJUČAK

Oklopljena kućišta imaju glavnu ulogu u očuvanju radnih perfomansi elektronskih sistema pod uticajem spoljašnjeg EM zračenja, kao i u eliminisanju ili redukovanju uticaja njihove emisije na sisteme u okruženju. Usled nesavršenosti u tehnološkom procesu izrade, potrebe za hlađenjem i odvođenjem viška toplote iz sistema, zahteva za pristupom sistemu u cilju napajanja energijom i dr, metalni zidovi ovih kućišta često poseduju otvore kojima se u slučaju zidova sa velikom električnom provodnošću dominatno ostvaruje EM sprega između struktura unutar oklopa i spoljašnjeg okruženja.

Uspešna primena diferencijalnih numeričkih metoda u vremenskom domenu za analizu praktičnih EMC problema zahteva tačnu i efikasnu karakterizaciju količine EM energije koja putem pojedinačnih i ventilacionih otvora prodire u prostor unutar i van oklopa. Pri tome je potrebno uzeti u obzir broj otvora, njihov oblik i električnu veličinu, međusobnu spregu kao i debljinu zidova u kojima se nalaze. Svi ovi faktori, ilustrovani u radu, manje ili više utiču na efikasnost oklopa i nivo curećeg EM zračenja te je, u zavisnosti od raspoloživih računarskih resursa i prirode problema, potrebno primeniti odgovarajući numerički (konvencionalni i/ili integralni) pristup u cilju njihovog kompletnog sagledavanja. U narednom periodu, autori planiraju detaljna numerička i eksperimentalna istraživanja uticaja svakog od ovih faktora na funkcije oklapanja sistema.

Literatura

[1] C. Christopoulos: Principles and Techniques of Electromagnetic Compatibility, CRC Press, 2000.

[2] K.S. Kunz, R. J. Luebbers: The Finite Difference Time Domain Method for Electromagnetics, CRC Press, Boca Raton, FL, 1993.

[3] C. Christopoulos: The Transmission-Line Modelling (TLM) Method, IEEE Press in association with Oxford University Press, Piscataway, NJ, 1995.

[4] A. J. Wlodarczyk, V. Trenkic, R. Scaramuzza, C. Christopoulos: “A fully integrated multiconductor model for TLM”, IEEE Transactions on Microwave theory and techniques, Vol. 46, No. 12, 1998, pp. 2431-2437.

[5] V. Trenkic, R. Scaramuzza: “Modelling of arbitrary slot structures using transmission line matrix (TLM) method”, Proceedings of International Symposium on Electromagnetic Compatibility, Zurich, Switzerland, pp. 393-396, 2001.

[6] N. Dončov, A. J. Wlodarczyk, R. Scaramuzza, V. Trenkić: “Compact TLM model of air-vents”, Electronics Letters, Vol. 38, No. 16, 2002, pp. 887-888.

[7] N. Dončov, B. Milovanović: “Capabilities of Empirical TLM Air-vent Model“, Proceedings of the 23rd International Review of Progress in Applied Computational Electromagnetics - ACES 2007, Verona, Italy, 2007, pp. 1525-1530.

[8] J. Joković, B. Milovanović, N. Dončov, “TLM Analysis of Cylindrical Metallic Cavity Excited with a Real Feed Probe”, International Journal of RF and Microwave Computer-Aided Engineering, John Wiley & Sons Inc., Vol. 16, No. 4, pp. 346-354, 2006.

[9] J. Joković, B. Milovanović, N. Dončov, “Numerical Model of Transmission Procedure in a Cylindrical Metallic Cavity Compared with Measured Results”, International Journal of RF and Microwave Computer-Aided Engineering, John Wiley & Sons Inc., Vol. 18, No. 4, 2008, pp. 295-302.

[10] M.P.Robinson, T.M.Benson, C.Christopoulos, J.F.Dawson, M.D.Ganley, A.C.Marvin, S.J.Porter, D.W.P.Thomas: “Analytical Formulation for the Shielding Effectiveness of Enclosures with Apertures”, IEEE Transactions on Electromagnetic Compatibility, Vol.40, No.3, 1998, pp. 240-248.

[11] M. Li, J. Nuebel, J. L. Drewniak, R. E. DuBroff, T. H. Hubing, T. P. Van Doren: “EMI from airflow aperture arrays in shielding enclosures – experiments, FDTD, and MoM modelling”, IEEE Transactions on Electromagnetic Compatibility, Vol. 42, No. 3, 2000, pp. 265-275.

Autori

Bratislav Milovanović je diplomirao (1972), magistrirao (1975) i doktorirao (1979) u oblasti mikrotalasne tehnike i antena na Elektronskom fakultetu u Nišu, gde i danas radi kao redovni profesor. Njegove oblasti istraživanja su mikrotalasna tehnika i tehnologije, primenjena i numerička elektromagnetika i neuronske mreže. Autor je ili koautor više od 500 naučnih radova, od čega je preko 40 objavljeno u vodećim međunarodnim časopisima i monografijama. Rukovodio je realizacijom preko 20 projekata u oblasti osnovnih i primenjenih istraživanja, s posebnim akcentom na strateški važne telekomunikacione projekte u oblasti tehnološkog razvoja. Član je Naučnog društva Srbije i redovni član Akademije inženjerskih nauka Srbije i Crne Gore. Predsednik je nacionalnog Udruženja za mikrotalasnu tehniku i tehnologije, predsednik MTT-S sekcije za Srbiju i Crnu Goru, potpredsednik predsedništva Društva za ETRAN, potpredsednik Stručnog saveta Republičke agencije za telekomunikacije i član Republičke komisije za akreditaciju i proveru kvaliteta. Član je međunarodnih stručnih udruženja (IEEE, EuMA, WISAS i ARFTG) i član Upravnog odbora Društva za telekomunikacije. U 2006. godini promovisan je u počasnog člana ETRAN društva. Osnivač je i predsednik Programskog i Organizacionog odbora ugledne međunarodne IEEE konferencije o telekomunikacijama – TELSIKS i ko-predsedavajući međunarodne konferencije ICEST. Prof. dr Bratislav Milovanović dobitnik je Oktobarske nagrade Grada Niša (1986) i trostruki dobitnik nagrade RTS (1985, 1994 i 1997) za naučne rezultate u oblasti telekomunikacija. Dobitnik je najvišeg priznanja nacionalnog Udruženja za mikrotalasnu tehniku i tehnologiju za razvoj mikrotalasne tehnike (1999). Nosilac je Povelje Elektronskog fakulteta u Nišu za doprinos razvoju fakulteta (1985) i Plakete Univerziteta u Nišu za doprinos razvoju Univerziteta (1989). Dobitnik je Povelje Elektrotehničkog fakulteta iz Banja Luke (2002), Povelje Fakulteta za telekomunikacije sa Tehničkog Univerziteta iz Sofije, Bugarska (2006), Nagrade Udruženja univerzitetskih nastavnika Srbije (2009) i Plakete Fakulteta tehničkih nauka u Novom Sadu za poseban doprinos razvoju fakulteta (2010).

Nebojša Dončov je diplomirao (1995), magistrirao (1999) i doktorirao (2002) u oblasti telekomunikacija na Elektronskom fakultetu u Nišu, gde i danas radi kao vanredni profesor. U periodu od 2001. do 2004. godine radio je kao razvojni i istraživački inženjer u Kompaniji Flomerics Ltd, Velika Britanija, u Odeljenju za elektromagnetiku (sada u CST-u), na poslovima razvoja komercijalnih programskih paketa Micro-stripes i FLO/EMC u oblasti elektromagnetike i elektromagnetske kompatibilnosti. Njegove trenutne oblasti istraživanja su numerička i primenjena elektromagnetika sa posebnim akcentom na razvoj i primenu TLM metoda u oblasti mikrotalasa, metamaterijala i elektromagnetske kompatibilnosti. Autor je ili koautor više od 100 naučnih radova od čega 10 objavljenih u vodećim međunarodnim časopisima. Dobitnik je nagrade “Young Scientist Award” dodeljene 2002. godine od strane internacionalnog udruženja URSI (International Union of Radio Science). Član je internacionalnog IEEE udruženja i Nacionalnog udruženja za mikrotalasnu tehniku i tehnologiju.

Vesna Milutinović je diplomirala 2000. godine na Elektronskom fakultetu u Nišu, smer elektronika i telekomunikacije. Doktorske studije na Elektronskom fakultetu u Nišu, odsek telekomunikacije, pod mentorstvom prof. dr. Bratislava Milovanovića, upisala je u oktobru 2008. godine. Radila je na poslovima planiranja, razvoja i projektovanja telekomunikacionih mreža. Od aprila 2007. godine zaposlena je u RATEL-u na poslovima vezanim za kontrolu radio-komunikacija. Autor je radova iz oblasti telekomunikacionih mreža i sistema.

Tatjana Cvetković je diplomirala 1989. godine u Zagrebu, na Vojno-tehničkom fakultetu, smer telekomunikacije. Od marta 2006. godine zaposlena je u Sektoru za informaciono-komunikacione tehnologije u RATEL-u na poslovima vezanim za pružanje telekomunikacionih usluga. Doktorske studije na Elektronskom fakultetu u Nišu, odsek telekomunikacije, pod mentorstvom prof. dr. Bratislava Milovanovića, upisala je u novembru 2008. godine. Autor je i koautor niza konferencijskih radova vezanih za pružanje i kvalitet telekomunikacionih usluga.